Grundlagen der Gleitreibung zwischen Festkörpern (Reibungstheorie)

Einführung

Festkörperreibung unter Relativbewegung zweier Körper zueinander spielt in einigen technischen Bereichen ein große Rolle. Als häufigstes Anwendungsgebiet sind sicherlich die verschiedenen Bremsanlagen von Fahrzeugen zu nennen, ebenso die lösbaren kraftschlüssigen Kupplungen bei Fahrzeugen mit Verbrennungsmotor. Verbreitet sind aber auch Gleitlager für Rotation und Linearbewegung, die ohne intern oder extern hinzugefügte flüssige Schmierstoffe funktionsfähig sind. Während bei Bremsanlagen und Kupplungen möglichst konstante und relativ hohe Reibwerte über alle Betriebspunkte erzielt werden sollen, besteht das Entwicklungsziel bei den genannten Gleitlagern in der Regel darin, die Reibwerte möglichst zu minimieren. Weitere Anforderungen bei allen diesen Anwendungsgebieten sind: Geringer Verschleiß und insbesondere bei Bremsanlagen: Höchstmögliche mechanische und thermische Sicherheit. Bisher gibt es keine theoretische Grundlage (Reibungstheorie), um den Reibwert zweier zueinander bewegter Festkörper ohne Versuche voraussagen zu können. Der Stand der Technik hat sich bisher aus Erfahrungswerten und Versuchen entwickelt. Ziel dieser Veröffentlichung ist es, diese theoretische Grundlage darzulegen, damit weitere Forschung darauf aufbauen kann.

1 Das primäre Prinzip der Festkörperreibung

Die Reibung zwischen zwei Festkörpern kann im Zustand mit oder ohne Relativbewegung zueinander (Gleitreibung oder Haftreibung) durch folgendes Modell beschrieben werden.

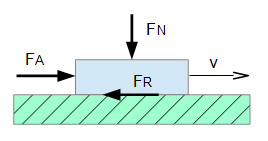
Dabei werden die ebenen Flächen zweier Körper durch eine senkrecht zwischen den Flächen wirkende Druckkraft F_N belastet, die häufig der Massenkraft des oberen Körpers unter Schwerkraft entspricht. Nach dem Coulombschen Gesetz besteht bei Haft- und bei Gleitreibung zwischen der Reibkraft F_R und der Kraft F_N für eine Materialpaarung definitionsgemäß jeweils ein konstantes Verhältnis, das als Reibwert µ bezeichnet wird, wobei die Größe der Reibkraft identisch mit der für die Bewegung erforderlichen Kraft F_A ist.

Es gilt also: µ = F_R / F_N

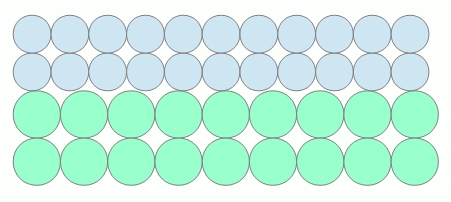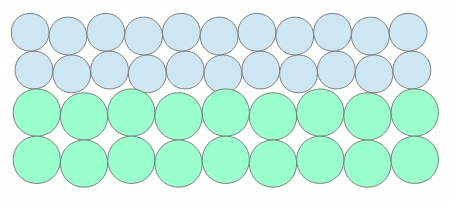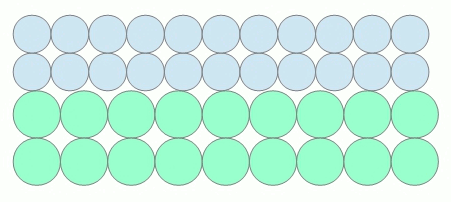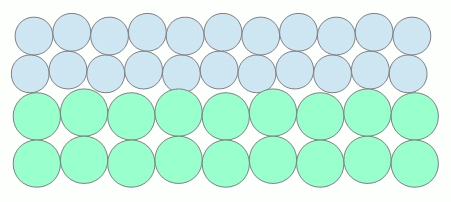
In der Wärmelehre wird die Energieübertragung durch Wärme im Kontaktbereich zweier Festkörper durch die temperaturabhängige Intensität der atomaren Schwingungen erklärt, die sich gegenseitig durch Impulsübertragung anregen. Im thermisch ausgeglichenen Zustand (beide Körper haben dieselbe Temperatur) sind die Energieströme zwischen den Körpern identisch.

Folgende bewegte Animation soll diesen Zustand prinzipiell darstellen.

Kombiniert man dieses Modell mit dem Modell der Coulombschen Reibungstheorie wird deutlich, dass die gegenüberliegenden Atome beider Körper im Kontaktbereich bei Temperaturen oberhalb des absoluten Nullpunktes in Relativbewegung zueinander stehen, auch wenn keine Relativbewegung im Makrobereich zwischen den Körpern (statischer Zustand) stattfindet. Im statischen Zustand wird die Kraft F_N über eine endliche Anzahl von Atomkontakten ohne weitere Energieübertragung aufgenommen. Ein einzelner Atomkontakt überträgt (zu einem Zeitpunkt) die Kraft ΔF_N. Hierbei hat die vektorielle Summe aller dieser Kräfte aus statistischen Gründen keine Komponente in Richtung der Kontaktebene.

Da die Gesamtenergiebilanz im statischen Zustand und bei thermischer Ausgeglichenheit gleich Null ist, muss der Impulsaustausch zwischen den einzelnen gegenüberliegenden Atomen quantitativ nicht näher betrachtet werden und im Zustand der Relativbewegung beider Körper zueinander ist deshalb nur die dadurch hinzukommende vektorielle Komponente beim Impulsaustausch relevant. In diesem Zustand erhält jede Atomschwingung des bewegten Körpers eine zusätzliche Richtungskomponente in Bewegungsrichtung. Das hat Auswirkung auf die sich gegenüberliegenden Atome im Kontaktbereich, die sich „im Wege stehen“ und – wie bereits erwähnt – einen individuellen Teil ΔF_N der Normalkraft F_N übertragen. Diese Schwingungskomponenten infolge der Bewegung können entsprechend der folgenden Abbildung in einen (roten) Anteil zerlegt werden, der durch das Zentrum des gegenüberliegenden Atoms verläuft und somit die innere Energie der Körper erhöht (das Temperaturniveau steigt) und einen (grünen) Anteil der widerstandslos tangential zur „Kugeloberfläche“ des Atoms verläuft. Im gleichen Verhältnis muss ein Anteil der individuellen Kraft ΔF_N aufgebracht werden, um diese Energie zuzuführen.

Die Darstellung der Atome als Kugeln erlaubt jedoch nicht, die Energieübertragung als nicht zentralen Impuls zweier Kugeln anzusehen, da es sich um den Kontakt zweier Kraftfelder handelt und nicht von materiellen Kugeloberflächen mit Reibung zueinander. Es wird also über den Abstand zwischen Kontaktpunkt und Atomkern kein Moment übertragen.

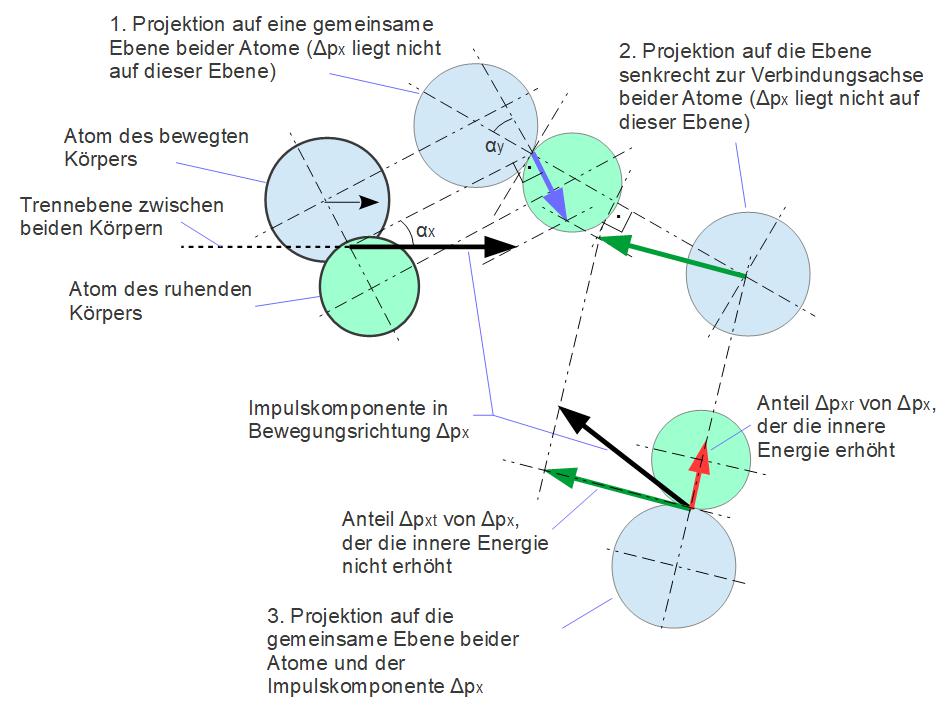
Der Betrag des (grünen) Vektors Δp_xt lässt sich über die rechtwinkligen Dreiecke, die durch die Vektoren gebildet werden, berechnen.

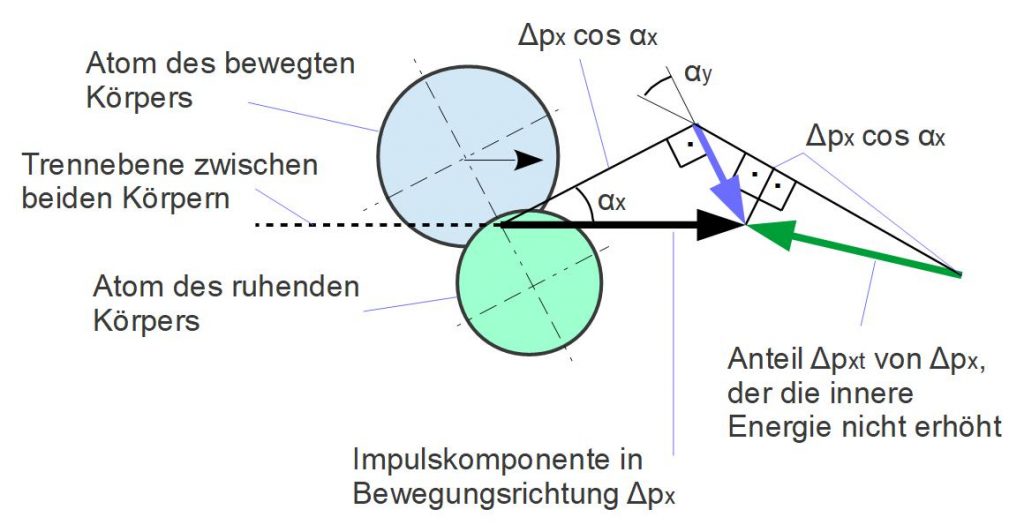
Der Betrag des (roten) Vektors Δp_xr kann anschließend über den Satz des Pythagoras ermittelt werden.

Dann erhält man folgendes Verhältnis zwischen Δp_xr und Δp_xt:

Bisher wurden nur diejenigen Konstellationen betrachtet, bei denen Atome des bewegten Körpers Atome des ruhenden passieren müssen. Statistisch gesehen gibt es aber genauso viele Paarungen, bei denen ein gegenüberliegendes Atom „bergab“ kontaktiert wird und dabei keine Impulskomponenten erzeugt werden, die zu einer Erhöhung der inneren Energie führen.

Es lässt sich ein primärer Reibwert µ_p definieren, der das Verhältnis zwischen der Summe aller roten und aller grünen individuellen Impulse darstellt. Der Gesamtreibwert µ_g beträgt dann:

µ_g = µ_p x µ_s

wobei µ_s der sekundäre Reibwert ist, der sich aus sekundären Effekten ergibt, die die Antriebskraft beeinflussen. Diese Effekte werden noch später angesprochen.

Um die Verteilung aller vorkommenden Impulse in Bezug zur Kontaktfläche zwischen zwei Körpern zu ermitteln, ist es sinnvoll die Winkelbezüge durch die auf die Kontaktebene projizierten Abstände x (Bewegungsrichtung) und y (senkrecht zur Bewegungsrichtung) der gegenüberliegenden Atompaare zu ersetzen.

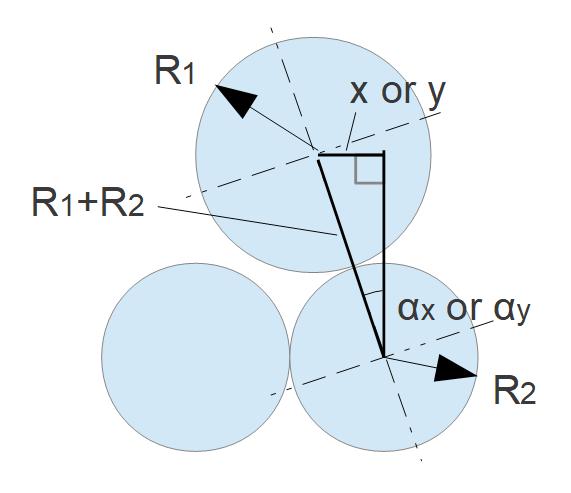
Dieses Modell geht allerdings davon aus, dass die Atome des „oberen“ Körpers die Freiheit besitzen, ungehindert in die „Täler“ zwischen den gegenüberliegenden Atomen einzutauchen, während die Atome des unteren Körpers ihre Lage nicht verändern. Das entspricht natürlich nicht der Realität.

Betrachtet man einen größeren Abschnitt zweidimensional, wird deutlich, dass sich die Atome auf jeden Fall aus ihrer umgebenden Struktur herausbewegen müssen, um mit dem gegenüberliegenden Atom in Kontakt zu kommen. Um herauszufinden, welcher der beiden Körper anpassungsfähiger ist, muss eine weitere physikalische Eigenschaft hinzugezogen werden, nämlich der Elastizitätsmodul. Je kleiner der E-Modul ist, desto nachgiebiger ist die Struktur. Wenn beide Körper unterschiedliche E-Module haben, dann passen sich die Atomstrukturen mit geringerem E-Modul stärker der Oberfläche des gegenüberliegenden Körpers an als umgekehrt. Das wiederum hat Auswirkung auf den größten auftretenden Winkel α_x bzw. α_y und damit auch auf die Strecke x bzw. y.

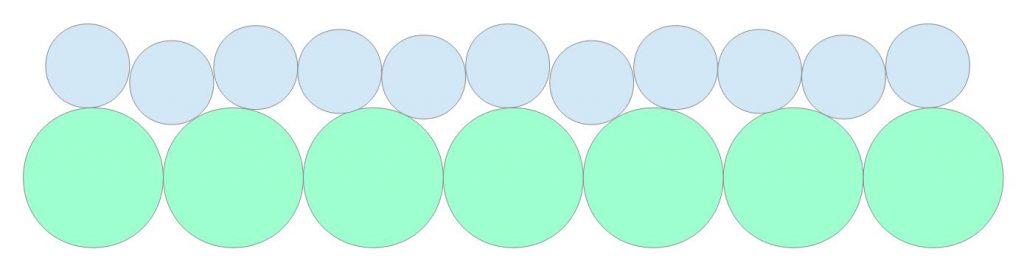
Das Modell zur Ermittlung der Abhängigkeit zwischen Kontaktwinkel α_x bzw. α_y und Strecke x bzw. y kommt immer dann den realen Verhältnissen nahe, wenn das obere Atom zu einem Material mit deutlich niedrigerem E-Modul gehört als das untere, was bei vielen technischen Anwendungen tatsächlich der Fall ist und noch später behandelt wird. Die Entwicklung eines Modells, das für beliebige Verhältnisse der E-Module zueinander gilt, wäre sicherlich wünschenswert, soll aber an dieser Stelle nicht weiter verfolgt werden.

Es gilt unter den genannten E-Modul-Verhältnissen:

Damit wird die Gleichung für Δp_xr / Δp_xt zu:

Diese Gleichung, aus der sich der primäre Gesamtreibwert µ_p berechnen ließe, soll hier nicht weiter allgemeingültig weiterentwickelt werden, da die Anwendung auf einen realen Fall nicht trivial ist, denn die Maximalwerte von x und y, die für die Berechnung des Integrals dieser Gleichung bekannt sein müssten, sind je nach Orientierung der gegenüberliegenden Atome zueinander unterschiedlich, wie folgende Extrembeispiele in der Draufsicht auf die Kontaktebene zeigen.

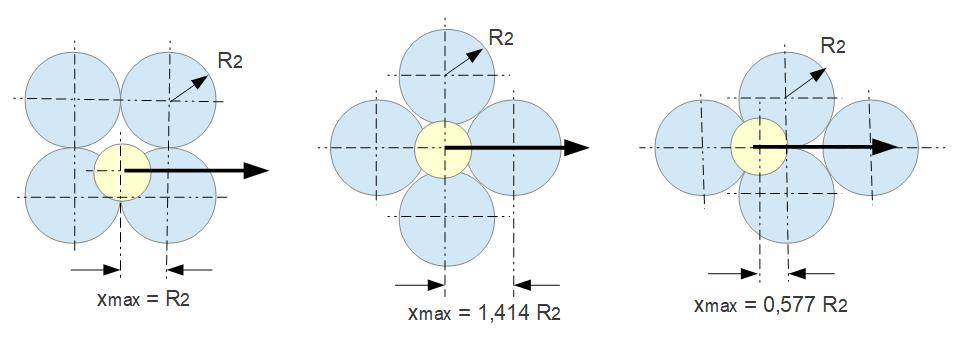
Im allgemeinen Fall bewegt sich das „obere“ Atom entlang einer beliebigen schrägen Geraden zur „unteren“ Atomstruktur.

Die Berechnung für einen realen Fall wird weiter dadurch erschwert, dass Materialien im Normalfall aus Molekülen mit verschiedenen Elementen bestehen, d.h. die Materialien bestehen aus Atomen mit unterschiedlichen Atomradien. Dabei ist auch zu berücksichtigen, ob die verschiedenen Elemente eines Materials alle mit derselben Wahrscheinlichkeit in Kontakt mit den Elementen des gegenüberliegenden Körpers kommen. Dies ist sicherlich auch abhängig von der Anordnung der Elemente innerhalb der Moleküle – manche Elemente befinden sich z.B. immer im Inneren eines Moleküls und können deshalb nie in direkten Kontakt mit dem gegenüberliegenden Körper kommen. Bei metallischen Oberflächen muss auch die Korrosionsschicht berücksichtigt werden, die immer vorhanden ist, wenn auch teilweise nur mit minimaler Schichtstärke. Dieses wichtige Thema wird an späterer Stelle behandelt. Des weiteren bestehen manche Materialien aus verschiedenen Molekülen, was die Lösung obiger Gleichung noch um ein vielfaches komplexer machen würde.

Das beschriebene primäre Prinzip der Festkörperreibung bezieht sich wie anfangs erwähnt nur auf den Zustand der Gleitreibung. Haftreibung unterliegt völlig anderen Gesetzmäßigkeiten, da keine Energieübertragung stattfindet. Deshalb ist auch die weit verbreitete Annahme falsch, dass die Haftreibung bei der Paarung zweier Feststoffe immer höher ist als die Gleitreibung. Es ist natürlich trivial, dass beim Beschleunigen aus dem Ruhezustand unter Haftreibung zunächst der Reibwert gleich bleiben oder geringer werden muss, sonst würde ja keine Relativbewegung beginnen. Trotzdem ist es möglich, dass mit zunehmender Relativgeschwindigkeit der Reibwert größer wird als der Haftreibwert. Die Haftreibung soll jedoch in dieser Abhandlung nicht weiter diskutiert werden.

2 Sekundäre Reibungseinflüsse

Neben der bisher behandelten primären Ursache der Reibung zwischen Festkörpern gibt es noch eine Vielzahl sekundärer Einflussgrößen, die in dem bereits aufgeführten Reibwert µs zusammengefasst werden können und je nach Materialpaarung sogar den Hauptanteil der Gesamtreibung ausmachen können. Diese sollen im Folgenden behandelt werden:

2.1 Reibung infolge von Verschleiß und plastischer Verformung

Sobald Verschleiß oder plastische Verformungen während der Bewegung an den Kontaktflächen auftreten, muss Arbeit aufwendet werden, um die Verschleißpartikel aus den Oberflächen herauszulösen bzw. um die erforderliche Verformungsenergie aufzubringen. Auf gleiche Weise wirken auch Verschweißvorgänge zwischen Materialien, die infolge der Bewegung aus einem der beiden Körper herausgerissen werden. In allen Fällen erhöht sich dadurch die Verschiebekraft FA. Diese Effekte haben einen besonders hohen Anteil am Gesamtreibwert bei Materialpaarungen mit beidseitig relativ hohem E-Modul wie Metalle oder Keramiken.

1949 haben Bowden und Taylor eine mathematisch-physikalisch bewiesene Theorie [1] veröffentlicht, nach der eine Relativbewegung zwischen zwei ungeschmierten Metallen in der Regel immer mit einer Verschweißung und anschließenden Loslösung der mikroskopisch kleinen Kontaktbereiche verbunden ist, was auch eine fortschreitende Zerstörung der Oberflächen zur Folge hat. Nach dieser Theorie lässt sich für einen weiten Bereich der Oberflächenbeschaffenheiten bezüglich Rauheit, Oxid- und Restfettanteilen ein sekundärer Reibwert von 0,16 bis 0,20 errechnen. Im Kontakt zwischen ungeschmierten Metallen kann sich in der Regel also die primäre Ursache der Gleitreibung gar nicht ausbilden, da jeglicher Kontakt zwischen gegenüberliegenden Atomen zur Zerstörung von atomaren Verbindungen führt. Das gilt interessanterweise selbst bei niedrigsten Belastungen.

2.2 Reibung infolge von Anziehungskräften

Zwei Materialien, deren Kontaktflächen eine qualitativ hochwertige Ebenheit aufweisen in Zusammenhang mit einer sehr geringen Rauhigkeit, weisen eine Anziehungskraft zueinander auf, die nicht vernachlässigbar ist und sich zur Druckkraft FN addiert und damit auch die Verschiebekraft FA erhöht. Dieser Effekt wird häufig der Adhäsion zugeschrieben. Es kann aber mit Hilfe der JKR-Theorie [2], die im Jahr 1971 entwickelt wurde, nachgewiesen werden, dass der Einfluß von Adhäsion bei realen technischen Anwendungen mit trockener Gleitreibung vernachlässigbar ist. Nach dieser Theorie ist bei Paarungen zwischen Metallen oder Keramiken und unverstärkten Kunststoffen (E-Modul ca. 2500 MPa) ein Einfluss von Adhäsion erst bei Oberflächenrauheiten unterhalb von Ra=0,06 µm relevant. Technische Oberflächen, die für Gleitpaarungen verwendet werden, haben aber in der Regel Rauhtiefen von Ra=0,2 und mehr. Es gibt allerdings Materialpaarungen, die ein Polieren der harten Gegenfläche verursachen (z.B. faserverstärkte Kunststoffe) und damit die Rauhigkeit im Laufe der Zeit vermindern, sodass möglicherweise doch ein Adhäsionseffekt zu Tragen kommt. Das wäre auch denkbar, wenn es eine Materialübertragung vom weichen auf das harte Material (z.B. bei PTFE-gefüllten Kunststoffen) gibt.

Eine weitere Ursache der Anziehungskraft zwischen zwei Körpern beruht zumindest anteilig auch auf folgender Tatsache: Bei Flächen, die tatsächlich in Kontakt miteinander sind, befindet sich keine Umgebungsluft mehr zwischen ihnen. Das bedeutet, dass der Umgebungsluftdruck nicht auf diese Flächen wirkt, aber weiterhin auf alle anderen Flächen der beteiligten Körper. Damit erhöht sich die Belastung zwischen den Kontaktflächen unter normalen Umgebungsbedingungen um 0,1 MPa. Allerdings muss bei realen Anwendungen wie z.B. bei ungeschmierten Kunststoff-Linearlagern, die sich auf metallischen Schienen bewegen, berücksichtigt werden, dass sich ein vollständiger Kontakt zwischen den gegenüberliegenden Flächen erst nach einer gewissen Zeit einstellt. Aufgrund von Fertigungstoleranzen (z.B. bei spritzgegossenen Gleitelementen) ist der Anteil der sich tatsächlich berührenden Kontaktflächen gegenüber der theoretisch zur Verfügung stehenden Fläche sehr gering. Mit zunehmender Laufstrecke passen sich jedoch die gegenüberliegenden Flächen infolge des kunststoffseitigen Verschleißes immer mehr an, bis ein im Rahmen der Schienenrauhigkeit möglicher vollständiger Kontakt erreicht ist.

Eine Erhöhung der Flächenpressung um 0,1 MPa ist nicht vernachlässigbar, da z.B. bei realen Anwendung mit ungeschmierten Lineargleitlagerungen die Flächenpressungen in den überwiegenden Fällen deutlich unter 1 Mpa liegen, wie folgende praxisnahe Berechnung zeigt:

Eine Maschine mit einer geeigneten ungeschmierten Linearführung mit Kunststoff-Gleitelementen soll 1 Jahr lang ununterbrochen mit einer mittleren Geschwindigkeit von 0,1 m/s laufen. Das entspricht 3154 km. Die Gleitelemente dürfen danach einen maximalen Verschleiß von 0,5 mm aufweisen. Sehr verschleißfeste Kunststoffe weisen eine Verschleißrate von 0,4 µm/km bei einer Flächenpressung von 1 MPa auf, wenn sie auf geeigneten Führungsbahnen laufen (z.B. der Kunststoff iglidur J200 der Fa. igus GmbH, Köln in Kombination mit einer harteloxierten Führungsschiene [3]) Es kann näherungsweise eine direkte Proportionalität zwischen Verschleißrate und Flächenpressung angenommen werden. Dann ergibt sich für diesen Fall eine zulässige Flächenpressung von:

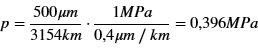
In diesem Fall würde sich also durch den Luftdruckeffekt die tatsächliche Flächenpressung nach einer Einlaufzeit um 0,1 Mpa und damit um 26% erhöhen. Das wäre ein Baustein für die Erklärung, warum der gemessene Reibwert bei vielen dieser Lagerungen mit zunehmendem Verschleiß steigt, obwohl im eigentlichen Sinn nicht der Reibwert sondern die tatsächliche Belastung steigt.

Dieser Effekt lässt sich minimieren, wenn eine der beiden Oberflächen einen vernachlässigbaren Verschleiß aufweist in Verbindung mit einer gewissen Rauhigkeit oder Welligkeit im Makrobereich, wodurch sichergestellt ist, dass die Umgebungsluft zu einem großen Anteil zwischen den sich berührenden Körpern verbleiben kann. Hohe Luftfeuchtigkeit wiederum kann zu einer Verstärkung des Luftdruckeffektes führen, wenn Wasser in den verbleibenden Zwischenräumen einen Teil der Luft verdrängt.

Es wäre auch denkbar, dass der Luftdruckeffekt Resonanzen und damit Geräusche verursacht, da der Effekt fast schlagartig aufhört, sobald der Materialkontakt unterbrochen wird (natürlich benötigt auch die Luft eine gewisse Zeit zum Einströmen). Ein erneuter Kontakt könnte in Zusammenhang mit dem Eigenschwingungsverhalten der Materialien einen ständig wiederkehrenden Kontaktverlust verursachen.

2.3 Reibung infolge von innerer Materialreibung

Ein weiterer sekundärer Effekt auf den Reibwert tritt bei Materialien auf, die einen hohen Dämpfungsgrad besitzen (wie z.B. Elastomere), der von einer freuquenzabhängigen inneren Reibung verursacht wird. Bei ein- oder beidseitiger elastischer Verformung der Kontaktzonen im Mikrobereich während der Relativbewegung infolge Rauheit muss dann Arbeit aufgewendet werden. Da dieser Effekt auch geschwindigkeitsabhängig ist, ist er möglicherweise die Erklärung für die starke Geschwindigkeitsabhängigkeit vieler tribologischer Paarungen mit Kunststoffen.

1963 hat Grosch eine Theorie [4] bezüglich der Gleitreibung zwischen Elastomeren und harten rauhen Oberflächen veröffentlicht, die bis heute bei der Entwicklung von Fahrzeugreifen verwendet wird. Bei dieser Theorie wird die Reibung infolge der Relativbewegung unmittelbar an den Kontaktstellen – also der primäre Reibwert – vernachlässigt, da bei technisch relevanten Anwendungen der sekundäre Reibwert infolge der elastischen Verformung des Elastomers deutlich überwiegt. Der Reibwertverlauf in Abhängigkeit von der Relativgeschwindigkeit erreicht dabei über einen weiten Geschwindigkeitsbereich ein Maximum und fällt außerhalb dieses Bereichs in beiden Richtungen stark ab.

2.4 Reibung infolge von inneren Kriechvorgängen, Phasenumwandlungen und statischer Aufladung

Als weitere sekundäre Effekte sind noch zu benennen:

– Geschwindigkeiten, die so langsam sind, dass Kriechvorgänge innerhalb eines Körpers (z.B. bei Kunststoffen) eine Rolle spielen (Quasi-Flüssigkeitsreibung) (z.B. bei Loslagern für Brücken mit der Gleitpaarung PTFE gegen Metall). Dabei wird im Kontaktbereich eine geringere Strecke zurückgelegt als im Makrobereich.

– partielle Phasenumwandlungen eines Materials während des Kontaktes mit dem Gegenkörper von fest nach flüssig (z.B. bei Eis). Dieser Effekt bewirkt eine Verbesserung des Gesamtreibwertes µg. Bei einer Phasenumwandlung infolge der gegenseitigen atomaren Anregungen wird die Impulskomponente, die ins Zentrum des gegenüberliegenden Atoms gerichtet ist, reversibel umgewandelt. Es kann hier nur vermutet werden, dass die Kraftkomponenten von ΔF_N, die für diese reversible Umwandlung aufgebracht werden, bei der reversiblen Rückumwandlung wieder in Summe in umgekehrter Richtung auftreten und somit erstere wieder aufheben.

– partielle Phasenumwandlungen eines Materials in Form einer Änderung der Kristallstruktur während des Kontaktes mit dem Gegenkörper (ein Effekt, der eventuell bei PTFE eine Rolle spielt, das bei 19°C und bei 35°C seine Kristallstruktur ändert und amorphe Bestandteile bei 127°C in eine unterkühlte Flüssigkeit übergehen²). Dieser Effekt bewirkt ebenfalls eine Verbesserung des Gesamtreibwertes µ_g und kann wie bei einer Phasenumwandlung von fest nach flüssig erklärt werden.

– statische Aufladung, wenn beide Körper nicht elektrisch leitend sind. Hierzu gibt es keine abgesicherten Erkenntnisse, ein Einfluss sollte aber nicht ausgeschlossen werden, solange die Wirkungslosigkeit nicht bewiesen ist.

3 Stark vereinfachtes Berechnungsbeispiel

Trotz der in Kapitel I beschriebenen Komplexität der realen atomaren Anordnungen an den Kontaktflächen zweier sich gegeneinander bewegenden Körper, wäre es doch interessant, einen vereinfachten Fall zu betrachten und den ungefähren Wert des primären Reibwertes zu ermitteln.

Deshalb soll der einfachsten Fall zweier Körper betrachtet werden, die jeweils nur aus einem Element bestehen. Dann kann man die zuletzt ermittelte Gleichung

lösen, wenn man für x_r und y_r mittlere Wertebereiche annimmt, die irgendwo zwischen dem größtmöglichen und dem kleinstmöglichen Bereich für x bzw. y liegen.

Da es keinen Grund dafür gibt, warum x und y unterschiedliche Bereiche annehmen werden, kann man sie auch gleichsetzen. Es gilt dann:

Der primäre Reibwert µ_p kann definiert werden als 50% (wegen der 50%igen „Bergabfahrt“ der Atome) des mittleren Verhältnisses von Δp_xr / Δp_xt bei Betrachtung dieses Verhältnisses über die Strecke x von x_max bis x=0.

Es soll angenommen werden, dass der Maximalwert von x_r im Mittel bei x_max=R₂ auftritt.

Dann gilt:

Es gilt also:

Diese Gleichung lässt sich nur numerisch lösen.

Es soll die Gleitpaarung Polyethylen (PE) gegen die eloxierte Oberfläche von Aluminium betrachtet werden. Damit ist auch die Bedingung eines großen Unterschiedes beim E-Modul zwischen beiden Körpern erfüllt (PE: 1.500 MPa und Al₂O₃: 406.000 MPa). PE hat die chemische Formel C₂H₄, wobei auf der Außenhülle des PE-Moleküls der Wasserstoff (Atomradius 32 pm) angeordnet ist, der deshalb und aus der Tatsache, dass er doppelt so oft vorkommt wie der Kohlenstoff, die mit Abstand größte Wahrscheinlichkeit hat mit der eloxierten Oberfläche in Kontakt zu kommen. Eloxal besteht aus Aluminiumoxid (Al₂O₃) mit einem Atomanteil von 40% Aluminium (Atomradius 143 pm) und 60% Sauerstoff (Atomradius 66 pm).

Würde man den primären Reibwert nur mit dem Atomradius vom Sauerstoff der Alumiumoxid-Oberfläche berechnen, ergäbe sich µ_p(O) = 0,160, mit dem ausschließlichen Atomradius von Aluminium ergäbe sich µ_p(AL) = 0,180. Bei anteilsmäßiger Gewichtung unter der Voraussetzung einer linearen Abhängigkeit ergibt sich dann für die eloxierte Oberfläche µ_p(Al₂O₃) = 0,172.

Um den dazugehörigen sekundären Reibwert µ_s theoretisch ermitteln zu können, fehlen noch weitestgehend die theoretischen Grundlagen für die beschriebenen Effekte. Nach erfolgreicher Berechnung des primären Reibwertes wäre man aber in der Lager, aus Versuchen zur Ermittlung des Gesamtreibwertes µ_g zumindest die Summe aller sekundären Reibwerte für eine Paarung unter bestimmten Betriebsbedingungen (Geschwindigkeit, Flächenpressung, Temperatur) indirekt zu ermitteln mit der Gleichung: µ_s = µ_g / µ_p

4 Besonderheiten bei metallischen Gleitpartnern

Wie bereits weiter oben erwähnt, treten bei Metallen unter normalen Umgebungsbedingungen immer Oxidationsvorgänge an der Oberfläche auf, d.h. die Metalle verbinden sich dort mit dem Sauerstoff der Luft zu Metalloxiden. Allerdings treten je nach Metall an der Oberfläche auch Reaktionen mit Kohlendioxid und/oder dem Wasserstoff aus der Luftfeuchtigkeit auf. An der äußersten Oberfläche der Oxidschicht werden hauptsächlich die der Atmosphäre entzogenen Elemente vorliegen. Jedes Metalloxid hat ein festgelegtes Verhältnis zwischen der Anzahl der Atome des Metallelementes und der Atome der oxidbildenden Elemente. Dadurch ergibt sich eine mehr oder weniger dichte Oberflächenschicht der oxidbildenden Elemente, was einen erheblichen Einfluss auf den primären Reibwert hat.

Es soll hier ein erster Vorschlag gemacht werden, den Einfluss dieses Effektes quantitativ abzuschätzen. Wenn man das Verhältnis der Projektionsflächen zwischen den oxidbildenden Atomen und den Metallatomen bildet, hat man ein Maß für die Anordnungsdichte der äußersten Oxidschicht gegenüber der Metallstruktur, die in der Regel eine sehr dichte Atomanordnung besitzt. Bei Zinkoxid (ZnO) beträgt dieses Verhältnis z.B. 24% oder bei Aluminiumoxid (Al₂O₃) 48%, das heißt, die relativ kleinen Sauerstoffatome haben relativ große Abstände mit großen Lücken zueinander, wodurch sich ein großer Anteil von ungünstigen Atomkontaktwinkeln bei Gleitreibung mit anderen Stoffen ergeben würde.

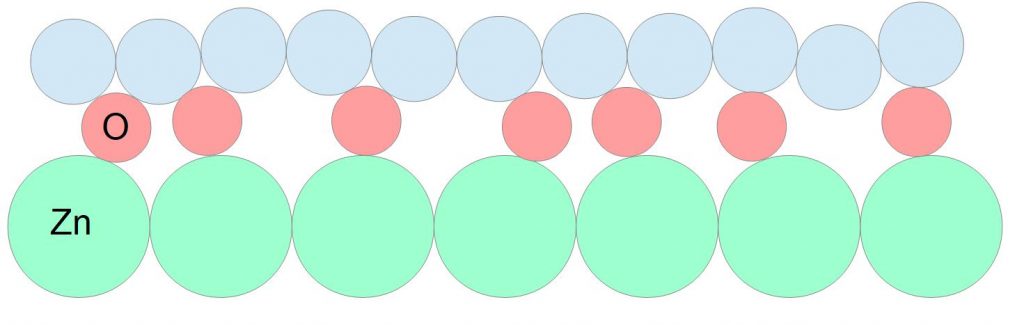
Bei Eisenoxid Fe(OH)₂ hingegen beträgt besagtes Verhältnis 242%, was bedeutet, dass sich am Eisenkristallgitter an der Oberfläche nicht an jedes Eisenatom eine (OH)₂-Gruppe anordnen kann, aber sich in jedem Fall eine ziemlich dichte Anordnung von (OH)₂-Molekülen bildet, was einen relativ guten Reibwert ergeben müsste. Tatsächlich haben Versuche gezeigt, dass Zink- und Aluminiumoberflächen relativ hohe Reibwerte verursachen, während Stahl- und Edelstahlflächen reibwertgünstiger sind.

Weitere Untersuchungen müssten auch klären, wie sich bei einer dauerhaften Gleitbewegung das Gleichgewicht zwischen Oberflächenverschleiß und Korrosionsschichtbildung quantitativ einstellt.

Metalloxide können auch gezielt durch technische Verfahren hergestellt werden, um einen besseren Schutz vor Korrosion zu erzeugen sowie dekorative Oberflächen. Entsprechend ist bei Aluminium das Eloxieren ein weit verbreitetes Verfahren. Die Anordnung der Sauerstoff- und der Aluminiumatome an der Oberfläche wird sich dabei sicherlich unterscheiden von der Oxidation unter Umgebungsluft. Erfahrungsgemäß haben eloxierte Oberflächen einen positiven Effekt bezüglich niedriger Reibung. Das deutet auf eine Oberfläche mit sehr dichter Atomanordnung hin.

5 Bedingungen für technisch geeignete trocken gleitende Systeme

Nicht jede Materialpaarung ist geeignet für trockene Relativbewegung zueinander. Je geringer die Anpassungsfähigkeit beider Körper zueinander ist, desto höher ist die spezifische Belastung auf die Körper. Das ist besonders bei Materialpaarungen der Fall, die beide einen relativ hohen E-Modul haben. Überschreitet die Belastung einen materialspezifischen Grenzwert, so wird das entsprechende Material an dieser Stelle zerstört. Hierdurch nimmt die Belastung auf andere Kontaktregionen weiter zu, was dann einen exponentiell steigenden Verschleiß zur Folge hat. Es gibt nicht viele Materialpaarungen, die unter der Voraussetzung geeigneter geometrischer Oberflächenqualität eine technisch akzeptable Verschleißrate haben und noch weniger, die auch hohe Relativgeschwindigkeiten zulassen. Da bei hoher Geschwindigkeit auch immer eine gute Wärmeleitung eines der beiden Materialien erforderlich ist, um die entstehende Reibungswärme abzuleiten, besteht eines der beiden Materialien in der Regel aus Metall oder Keramik, die beide einen relativ hohen E-Modul haben und das Gegenstück aus einem Material mit deutlich niedrigerem E-Modul, um sich bestmöglich an die Oberfläche des Partners anzupassen.

Nachwort

Dynamische Festkörperreibung existiert in der uns gewohnten Erscheinung in den meisten Fällen nur deshalb, weil die Oberflächen aller Festkörper mikroskopisch aus einer Aneinanderreihung von schwingenden Kugelabschnittsflächen bestehen.

Quellen:

[1] Valentin L. Popov, Kontaktmechanik und Reibung 3. Auflage 2015 S.164 ff

[2] K. L. Johnson, K. Kendall, A. D. Roberts: Surface energy and the contact of elastic solids. In: Proc. R. Soc. Lond. A. Band 324, Nr. 1558, 1971, S. 301 ff

[3] Untersuchungen des Verfassers im Rahmen langjähriger industrieller Entwicklungstätigkeit

[4] K. A. Grosch, The Relation between the Friction and Visco-Elastic Properties of Rubber. Proceedings of the Royal Society of London, Series A, Mathematical and Physical Sciences, 1963, Vol. 274, No. 1356, S. 21 ff

[5] Stefan Kirchberg, Ermittlung der elastischen Eigenschaften von PTFE und PTFE-Compounds mittels Dynamisch-Mechanischer-Analyse (DMA), GRIN Verlag 2016

Autor: Horst Moshammer, Am Sändchen 8, 53545 Linz am Rhein, Germany, dry-friction@web.de

2. Veröffentlichung: 18.03.2021 (1. Veröffentlichung war 30.11.2020)

Englische Version

weitere tribologische Veröffentlichungen