(Translation from the German Original)
Introduction
Dry friction between two bodies under relative movement is crucial in some technical fields. The most common application areas are certainly the various braking systems of vehicles, as well as the clutches in vehicles with combustion engines. Also sliding bearings for rotation and linear movement, which work without external or internal liquid lubrication are widespread. While the coefficient of friction at braking systems and clutches should be mainly constant and rather high at all operating points, the development target of sliding bearings is normally a low coefficient of friction. Further requirements for all of this application areas are: low wear and especially for braking systems: a very high mechanical and thermal safety.
So far, there is no theoretical basis to forecast the coefficient of friction of two solid bodies moving relative to each other without experiments. The state of the art has so far developed from empirical values and tests. It is the target of this publication to offer this theoretical basis so that further research can build on it.
1 The Primary Principle of Dry Friction
The friction between two solids can be described in the state with or without relative movement to each other (sliding friction or static friction) by the following model.
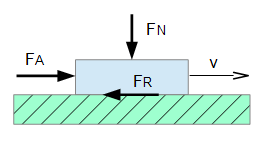
Here the flat surfaces of two bodies are loaded by a vertical pressure force FN, which often corresponds to the inertia force of the upper body under gravity. According to the law of Coulomb, there is a constant ratio by definition between the friction force FR and the load FN for every material combination for sliding friction and as well as for static friction, named the coefficient of friction µ, whereby the magnitude of the friction force is identical with the moving force FA.
Therefore it is: µ = FR / FN
In the theories of heat transfer, the energy transfer through heat in the contact area of two solid bodies is explained by the temperature-dependent intensity of the atomic oscillations, which stimulate each other through pulse transfer. In a thermally balanced state (both bodies have the same temperature) the flow of energy from one body to the other is identical in both directions. This is shown in principle with the following animation:

By combination of this theory with the law of Coulomb, it becomes clear that the opposite atoms of both bodies in the contact area are in relative movement to each other at temperatures above absolute zero, even if there is no relative movement at the macroscopic level between the bodies (static condition). In the static condition, the force FN is absorbed by a finite number of atom contacts without any further energy transfer. A single atomic contact transmits (at a time) the force ΔFN. For statistical reasons, the vector sum of all these forces has no component along the contact plane.
Because the total energy balance in the static and thermal balanced condition is zero, the impulse exchange between the single opposite atoms does not need to be considered quantitatively and therefor in the condition of relative movement of the two bodies to each other, only the hereby caused vectorial component is relevant in the impulse exchange. In this condition, every atomic oscillation of the moving body receives an additional component in the direction of movement. This has an effect to the opposite atoms in the contact area, which have to be passed and – as already mentioned – transfer an individual part ΔFN of the normal force FN. According to the following figure these oscillation components caused by the movement can be resolved in a (red) part directed to the center of the opposite atom and so increases the internal energy of the bodies (temperature increases) and a (green) part directed tangential along the atomic “spherical surface” without resistance. A proportion of the individual force ΔFN must be provided in the same ratio in order to supply this energy.
However, the representation of the atoms as balls does not allow the energy transfer to be viewed as a non-central impact of two balls, because it is a contact between two force fields and not between material balls with friction to each other. So no moment is transmitted over the distance between the contact point and the atomic center.
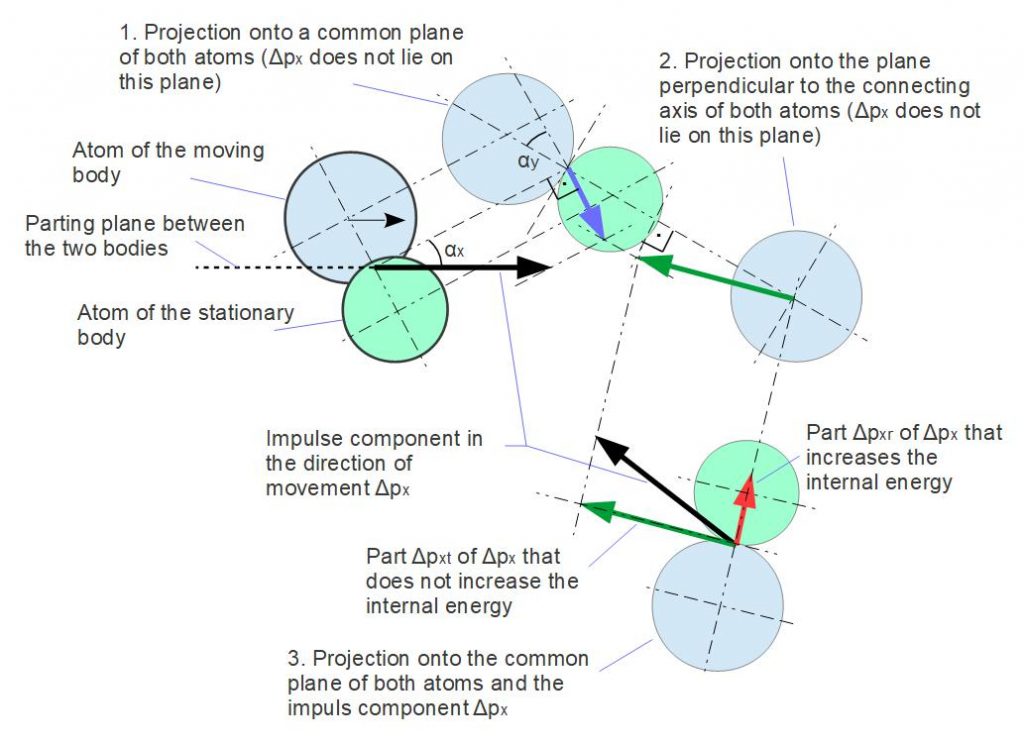
The amount of the (green) vector Δpxt can be calculated from the right-angled triangles formed by the vectors.

The amount of the (red) vector Δpxr can then be determined using the Pythagorean theorem.
Then the following relationship between Δpxr and Δpxt is obtained:
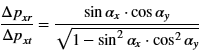
So far only those constellations have been considered in which atoms of the moving body have to pass atoms of the resting body. Statistically, however, there are just as many pairings in which an opposite atom is contacted “downhill” generating thereby no impact component to increase the inner energy.
A primary coefficient of friction µp can be defined, which represents the ratio between the sum of all red and all green individual impacts. The total coefficient of friction µg is then:
µg = µp x µs
where µs is the secondary coefficient of friction resulting from secondary effects influencing the moving force. These effects will be discussed later.
In order to determine the distribution of all impacts between two bodies in relation to the contact area it is useful to replace the angular references by the distances x (direction of movement) and y (perpendicular to the direction of movement) between the opposing pairs of atoms projected onto the contact plane.
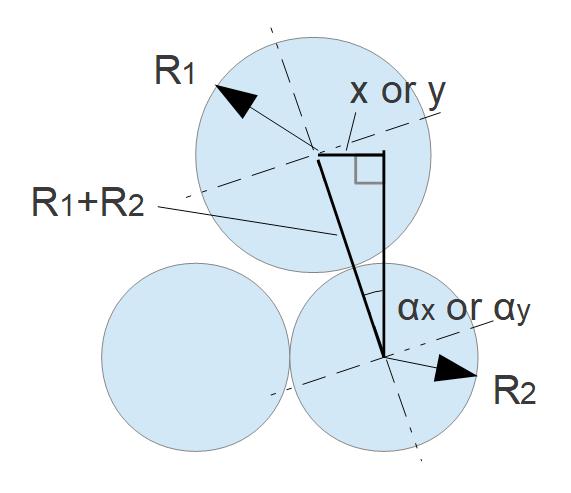
However, this model assumes that the atoms of the “upper” body are free to immerse themselves in the “valleys” between the opposing atoms, while the atoms of the lower body do not change their position. Of course, this does not correspond to reality.
Looking at a larger section two-dimensionally, it becomes clear that the atoms must certainly move out of their surrounding structure in order to come into contact with the opposite atom. To find out which of the two bodies is more flexible, another physical property has to be taken into account, namely the modulus of elasticity. The smaller the modulus of elasticity, the more flexible is the structure. If both bodies have different E-modules, then the atomic structures with a lower E-module adapt more to the surface of the opposite body than vice versa. This in turn has an effect on the largest occurring angle αx or αy and thus also on the distance x or y.
The model for determining the relationship between the contact angle αx or αy and the distance x or y comes close to the real conditions when the upper atom belongs to a material with a significantly lower E-module than the lower one, which is actually the case in many technical applications and will be discussed later. The development of a model that applies to any relationship between the E-modules would certainly be desirable, but should not be pursued further at this point.
The following applies under the mentioned E-module ratios:
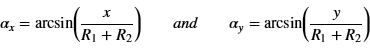
So the equation for Δpxr / Δpxt will change to:
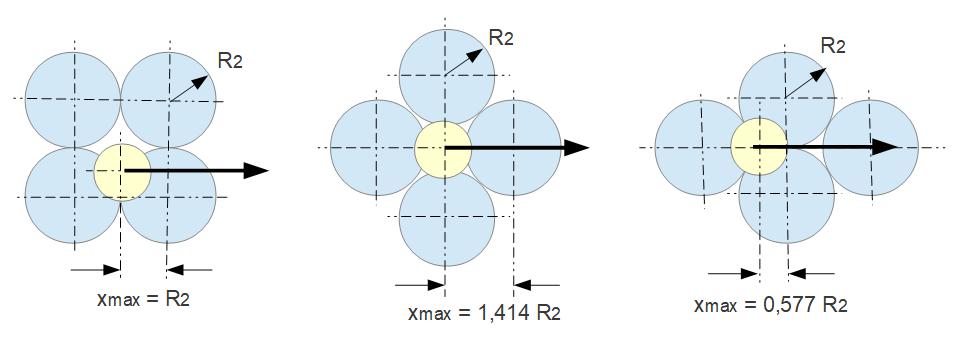
This equation, from which the primary coefficient of friction µp could be calculated, should not be further developed here in a generally applicable manner, since the application to a real case is not trivial, because the maximum values of x and y that have to be known for calculating the integral of this equation are different depending to the orientation of the opposing atoms, as the following extreme examples show in the top view at the contact plane.
In the general case, the “upper” atom moves along any oblique line to the “lower” atomic structure.
The calculation for a real case is even more difficult by the fact that materials normally consist of molecules with different elements, i.e. the materials consist of atoms with different atomic radii. It must also be taken into account whether the various elements of a material all come into contact with the elements of the opposite body with the same probability. This is certainly also dependent on the arrangement of the elements within the molecules – some elements are e.g. always inside a molecule and can therefore never come into direct contact with the opposite body. In the case of metallic surfaces, the corrosion layer must also be taken into account, which is always present, if only sometimes with a minimal layer thickness. This important topic will be discussed later. Furthermore, some materials consist of different molecules, which would make the solution of the above equation even more complex.
As mentioned at the beginning, the described primary principle of dry friction only relates to the state of sliding friction. Static friction is subject to completely different laws, since no energy transfer takes place. Therefor the widespread assumption is wrong that the static friction between two solid bodies is always higher than the sliding friction. It is of course trivial that when accelerating from the state of rest under static friction, the coefficient of friction must initially remain the same or decrease, otherwise no relative movement would begin. Nevertheless, it is possible that, with increasing relative speed, the coefficient of friction becomes greater than the coefficient of static friction. The static friction however, will not be discussed further in this publication.
2 Secondary Frictional Influences
In addition to the primary cause of dry friction between solids that has been dealt with so far, there are also a number of secondary influencing variables that can be summarized in the already mentioned secondary coefficient of friction µs and, depending on the material pairing, can even make up the main part of the total friction. These are considered in the following:
2.1 Friction due to Wear and Plastic Deformation
As soon as wear occurs on the contact surfaces during movement, work has to be expended to detach the wear particles from the surfaces. Welding processes between materials that are ripped out of one of the two bodies as a result of movement also act in the same way. In both cases, this increases the moving force FA. These effects have a very high proportion of the total coefficient of friction in the case of material pairings with a relatively high modulus of elasticity on both sides, such as metals or ceramics.
In 1949 Bowden and Taylor published a mathematically-physically proven theory [1], according to which a relative movement between two unlubricated metals is usually always associated with welding and subsequent detachment of the microscopic contact areas, which also results in progressive destruction of the surfaces. According to this theory, a secondary coefficient of friction between 0.16 and 0.20 can be determined for a wide range of surface conditions regarding to roughness, oxide deposits and residues of fat. In the contact between unlubricated metals, the primary cause of sliding friction cannot develop therefore at all, since any contact between opposing atoms leads to the destruction of atomic connections. Interestingly, this applies even to the lowest loads.
2.2 Friction due to Attractive Forces
Two materials, which have contact surfaces with a high-quality flatness in connection with a very low roughness, have a „force of attraction“ to each other that is not negligible and adds to the compressive force FN and thus also increases the moving force FA. This effect is often ascribed to adhesion. However, with the JKR theory [2] developed in 1971 it can be demonstrated that the influence of adhesion is negligible in real technical applications with dry sliding friction. According to this theory, in the case of pairings between metals or ceramics and unreinforced plastics (e-modulus approx. 2500 MPa), the influence of adhesion is only relevant if the surface roughness is below Ra = 0.06 µm. Technical surfaces that are used for sliding, however, usually have roughness depths of Ra = 0.2 µm and more. However, there are material pairings that polish the hard counter surface (e.g. fiber-reinforced plastics) and thus reduce the roughness over time, so that an adhesion effect may still occur. This can also happen when material is transferred from the soft to the hard material (e.g. with PTFE-filled plastics).
Another cause of the attraction between two bodies is at least partially based on the following fact: Surfaces that are actually in contact with each other no longer have any ambient air between them. This means that the ambient air pressure does not act on these surfaces, but continues to act on all other surfaces of the bodies involved. So the load between the contact surfaces under normal ambient conditions increases by 0.1 MPa. However, in real applications such as unlubricated plastic linear bearings that move on metallic rails, it must be taken into account that complete contact between the opposing surfaces only occurs after a certain time. Due to manufacturing tolerances (e.g. in the case of injection-molded sliding elements), the proportion of actually touching contact surfaces is very small compared to the theoretically available surface. As the running distance increases, however, the opposing surfaces adapt more and more due to the wear on the plastic side until complete contact is achieved, as far as this is possible due to the rail roughness.
An increase of the pressure by 0,1 MPa is not negligible, since e.g. in real applications with unlubricated linear plain bearings, the surface pressures are in the majority of cases well below 1 Mpa as the following practical calculation shows:
A machine with a suitable unlubricated linear guide with plastic sliding elements should run continuously for 1 year at an average speed of 0.1 m/s. That corresponds to 3154 km. The sliding elements may then show a maximum wear of 0.5 mm. Very wear-resistant plastics have a wear rate of 0.4 µm/km at a surface pressure of 1 MPa if they run on suitable guideways (e.g. the plastic material iglidur J200 from igus GmbH, Cologne, Germany in combination with a hard-anodized rail [3]) A direct proportionality between wear rate and surface pressure can be assumed approximately. In this case, there is a permissible surface pressure of:
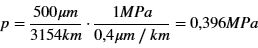
In this case, the air pressure effect would increase the actual surface pressure after a running-in period by 0.1 MPa and thus by 26%. That may be a component in explaining why the measured coefficient of friction in many of these bearings increases with increasing wear, although in the real sense it is not the coefficient of friction but the actual load that increases.
This effect can be minimized if one of the two surfaces shows negligible wear in connection with a certain roughness or waviness in the macro range, which ensures that a large proportion of the ambient air can remain between the bodies in contact. High humidity, on the other hand, can lead to an increase of the air pressure effect if water displaces a part of the air in the remaining spaces.
It is also imaginable that the air pressure effect causes resonances and thus noises, since the effect stops almost suddenly as soon as the material contact is interrupted (of course the air also needs a certain time to flow in). A renewed contact could cause a recurring loss of contact through the resonance behavior of the materials.
2.3 Friction due to internal material friction
Another secondary effect on the coefficient of friction occurs with materials that have a high degree of damping (such as elastomers), which is caused by frequency-dependent internal friction. In the case of elastic deformation of the contact zones on one or both sides in the micro range during the relative movement due to roughness, energy must be expended then. Because this effect is also speed dependent, it is possibly the explanation for the strong speed dependence of many tribological pairings with plastics.
In 1963 Grosch published a theory [4] relating to the sliding friction between elastomers and hard, rough surfaces, which is still today used in the development of vehicle tires. In this theory, the friction due to the relative movement directly at the contact points – i.e. the primary coefficient of friction – is neglected, since in technically relevant applications the secondary coefficient of friction due to the elastic deformation of the elastomer clearly predominates. The coefficient of friction as a function of the relative speed reaches a maximum over a wide speed range and falls sharply in both directions outside this range.
2.4 Friction due to internal creeping, phase transformation and Static Charging
Other secondary effects to be mentioned are:
– Speeds that are so slow that creeping processes within a body (e.g. with plastics) play a role (quasi-fluid friction) (e.g. floating bearings for bridges with the sliding pairing PTFE against metal). A shorter distance is covered in the contact area than in the macro area thereby.
– Partial phase transformations of a material during contact with the opposing body from solid to liquid (e.g. with ice). This effect causes an improvement in the overall coefficient of friction µg. In the case of a phase transformation due to mutual atomic stimulations, the impact component that is directed to the center of the opposite atom is reversibly converted. It can only be assumed here that the force components of ΔFN, which are needed for this reversible conversion, finally will be neutralized by forces which occur when the phase transformation reverses.
– Partial phase transformations of a material in the form of a change in the crystal structure during contact with the counter body (an effect that may play a role at PTFE, which changes its crystal structure at 19 °C and 35 °C and amorphous components at 127 °C pass over in a supercooled liquid [5]). This effect also improves the overall coefficient of friction µg and can be explained like the phase transformation from solid to liquid.
– Static charge, if both bodies are not electrically conductive. There are no reliable theories about this, but an influence should not be excluded as long as the irrelevance is not proven.
3 Simplified Calculation Example
Despite the complexity of the real atomic arrangements on the contact surfaces of two bodies moving against each other described in Chapter I, it would be interesting to consider a simplified case and to determine the approximate value of the primary coefficient of friction.
Therefore, the simplest case of two bodies, each consisting of only one element, shall be considered. Then the last determined equation
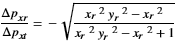
can be solved, if mean value ranges for xr and yr are assumed that lie somewhere between the largest and the smallest possible range for x and y.
Since there is no reason why x and y will assume different ranges, they can also be equated. The following then applies:
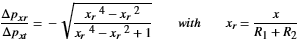
The primary coefficient of friction µp can be defined as 50% (because of the 50% “downhill” of the atoms) of the mean ratio of Δpxr / Δpxt when considering this ratio over the distance x from xmax to x = 0.
It should be assumed that the maximum value of xr occurs on average at xmax = R2.
Then applies:

and further:
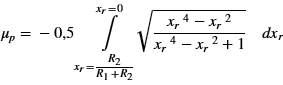
This equation can only be solved numerically.
The sliding pairing of polyethylene (PE) against the anodized surface of aluminum should be considered. This also fulfills the requirement of a large difference in the modulus of elasticity between the two bodies (PE: 1,500 MPa and Al2O3: 406,000 MPa). PE has the chemical formula C2H4, whereby the hydrogen (atomic radius 32 pm) is arranged on the outer shell of the PE molecule, which therefore and from the fact that it occurs twice as often as carbon, has by far the greatest probability to come into contact with the anodized surface. The anodized surface consists of aluminum oxide (Al2O3) with 40% aluminum atoms (atomic radius 143 pm) and 60% oxygen atoms (atomic radius 66 pm).
If calculating the primary coefficient of friction only with the atomic radius of the oxygen on the aluminum oxide surface, the result would be µp(O) = 0.160, with the atomic radius of aluminum only it would be µp(Al) = 0.180. With proportional weighting and assuming a linear dependency we get µp(Al2O3) = 0.172 for the anodized surface.
In order to determine the associated secondary coefficient of friction µs theoretically, the theoretical basis for the effects described is still largely missing. After successfully calculating the primary coefficient of friction, however, it would be possible to determine the sum of all secondary coefficients of friction indirectly by measuring the total coefficient of friction µg for a pairing under certain operating conditions (speed, surface pressure, temperature) using the equation: µs = µg / µp
4 Special Characteristics of Metallic Sliding Partners
As already mentioned above, under normal ambient conditions, oxidation processes always occur on the surface of metals, i.e. the metals combine there with the oxygen of the air to form metal oxides. However, depending on the metal, reactions with carbon dioxide and / or the hydrogen from the air humidity also occur on the surface. The elements withdrawn from the atmosphere will mainly be present on the outermost surface of the oxide layer. Every metal oxide has a fixed ratio between the number of atoms of the metal element and the atoms of the oxide-forming elements. This results in a more or less dense surface layer of the oxide-forming elements, which has a significant influence on the primary coefficient of friction.
A first suggestion should be made here to quantitatively estimate the influence of this effect. By building the ratio of the projected areas between the oxide-forming atoms and the metal atoms, a measure of the arrangement density of the outermost oxide layer in relation to the metal structure, which normally has a very dense arrangement of atoms, can be created . In the case of zinc oxide (ZnO) this ratio is e.g. 24% or 48% for aluminum oxide (Al2O3), that means, that the relatively small oxygen atoms have relatively large distances with large gaps between, which would result in a large proportion of unfavorable atomic contact angles in the case of sliding friction with other substances.

For iron oxide Fe(OH)2, on the other hand, the ration in question is 242%, which means that on the surface of the iron crystal lattice, an (OH)2-group cannot be arranged at every iron atom, but certainly there will be a fairly high dense arrangement of (OH)2 molecules, which should result in a relatively good coefficient of friction. In fact, tests have shown that zinc and aluminum surfaces tend to cause high coefficients of friction, while steel and stainless steel surfaces are more favorable.
Further studies would also have to clarify how the equilibrium between surface wear and corrosion layer formation is established quantitatively at permanent sliding movement.
Metal oxides are also specifically produced technically in order to protect against corrosion and to create decorative surfaces. Accordingly, anodizing is a widely used process for aluminum. The arrangement of the oxygen and aluminum atoms on the surface will certainly differ from the oxidation in ambient air. Experience has shown that anodized surfaces have a positive effect in terms of low friction. This indicates a surface with a very dense atomic arrangement.
5 Requirements for Technically Suitable Dry Sliding Systems
Not every material pairing is suitable for dry relative movement to one another. The less the two bodies are able to adapt to one another, the higher is the specific load on the bodies. This is especially the case with material pairings that both have a relatively high modulus of elasticity. If the load exceeds a material-specific limit value, the corresponding material is destroyed at this point. This further increases the load on other contact regions., which then results in exponentially increasing wear. There are not many material pairings that have a technically acceptable wear rate under the condition that the geometrical surface quality is suitable, and even fewer that also allow high relative speeds. Since good heat conduction from one of the two materials is always required at high speed in order to dissipate the resulting frictional heat, one of the two materials usually consists of metal or ceramic, which both have a relatively high modulus of elasticity. The other material normally has a significantly lower modulus of elasticity in order to adapt as best as possible to the surface of the partner.
Epilogue:
Dynamic sliding friction between solid bodies exists in its familiar appearance mostly because their surfaces consist, microscopically, of an arrangement of oscillating spherical segments.
Citations:
[1] Valentin L. Popov, Contact Mechanics and Friction 2017 page164 ff
[2] K. L. Johnson, K. Kendall, A. D. Roberts: Surface energy and the contact of elastic solids. In: Proc. R. Soc. Lond. A. Band 324, Nr. 1558, 1971, page 301 ff
[3] Investigations by the author during many years of industrial development activity
[4] K. A. Grosch, The Relation between the Friction and Visco-Elastic Properties of Rubber. Proceedings of the Royal Society of London, Series A, Mathematical and Physical Sciences, 1963, Vol. 274, No. 1356, page 21 ff
[5] Stefan Kirchberg; free translation from German: Determination of the elastic properties of PTFE and PTFE compounds using dynamic mechanical analysis (DMA) – [Ermittlung der elastischen Eigenschaften von PTFE und PTFE-Compounds mittels Dynamisch-Mechanischer-Analyse (DMA)]; GRIN Verlag 2016
Author: Horst Moshammer, Am Sändchen 8, 53545 Linz am Rhein, Germany, dry-friction@web.de
2. Publication: 03-18-2021 (1. Publication has been 11-30-2020)